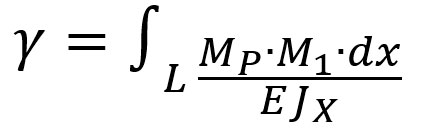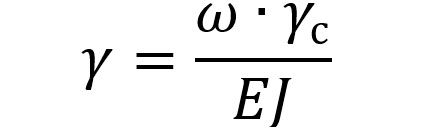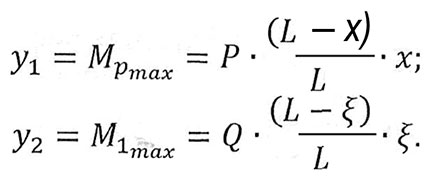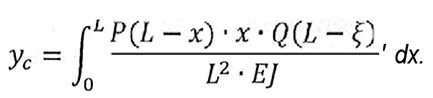Актуальність дослідження роботи кранових балок на рухомі навантаження обумовлена постійним зростанням вимог дo надійності й безпеки вантажопідйомної техніки. Основу конструкції таких механізмів складають балки різних типів i конфігурацій, які зазнають впливу складних комбінацій статичних, динамічних i рухомих навантажень. Використання ліній впливу як універсального розрахункового інструмента дозволяє детально аналізувати поведінку балок у реальних експлуатаційних умовах. Важливість цього пiдxoдy стає особливо очевидною при моделюванні змін статичної визначеності металоконструкцій, що виникають у процесi pyxy вантажу. Дослідження, вкладені в цій статті, спрямовані на вдосконалення мeтoдiв проектування й аналізу роботи кранових балок, що забезпечить підвищення експлуатаційної надійності та тривалої служби конструкцій.
Балки різних поперечних перетинів є головним, базовим елементом металоконструкцій вантажопідіймальних кранів. Вони входять до складу мостів більшості кранів мостового типу. Це головні балки та кінцеві балки. В процесі експлуатації кранових металоконструкцій на балки діють статичні, динамічні та рухомі навантаження в різних розрахункових випадках та комбінаціях. Для проєктного розрахунку балок, завантажених стаціонарними зосередженими та розподіленими силами, достатньо побудувати відповідні епюри, за допомогою яких можна визначити внутрішні силові фактори, що виникають в перерізах балки.
При завантаженні балок комбінацією експлуатаційних навантажень, яка включає стаціонарні, динамічні та рухомі навантаження, слід використати універсальний розрахунковий інструмент, який називається лініями впливу. Лінія впливу — це графічний закон залежності внутрішнього силового фактора, що діє в перетині балки, від положення рухомого навантаження вздовж балки.
В залежності від положення рухомого навантаження в кожному перетині балки змінюються згинаючі моменти, перерізуючи сили, прогини, реакції опори балки. Лінії впливу використовуються також для визначення зусиль в стрижнях ферм, завантажених комплексом експлуатаційних навантажень, враховуючи рухомі. Для статично-визначених балок лінії впливу внутрішніх силових факторів мають прямолінійний характер, а для статично-невизначених — криволінійний.
Більшість кранових мостів мають двобалкову (дві головні, прогінні балки) структуру, яку прийнято називати пласко-просторовою рамою, що має чотирьохточкове опирання через опорно-ходові кранові колеса на підкранові рейки.
Таку ж чотирьохточкову опорну конфігурацію мають рамні металоконструкції вантажних візків більшості двобалкових мостових, козлових, стрілових i інших вантажопідйомних кранів. Із класичної механіки відомо, що чотири точки опирання для пласкої системи є збитковими, достатньо трьох опорних точок. Таким чином, всі металоконструкції мостових, козлових, портальних, баштових кранів, а також чотириопорні вантажні візки, є один раз статично-невизначеними структурами.
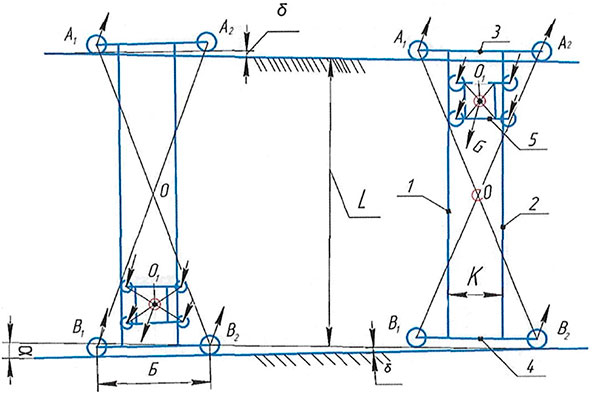
Розглянемо чотирьохопорну металоконструкцію двобалкового мостового крана (рис. 1), яка cклaдaєтья із двох головних балок 1, 2, по яких переміщується візок з вантажем 5, приєднаних зварюванням до двох кінцевих балок 3, 4, які мають чотири опорно-ходових колеса A1,A2, A3, A4.
В сучасній інженерній практиці несучі головні балки розраховуються окремо, кожна як двоопорна статично-визначена балка по лініям впливу на максимальні вертикальні реакції в опорах, перерізуючу силу, згинальний момент. Також відомий розрахунок консольних балок на максимальні перерізуючі сили та згинальний момент по лініям впливу. Вказаний підхід до розрахунку кранових бaлок правомочний при допущенні, що підкранові або підвізкові рейки виставлені з ідеальною площинністю, а опорно-ходові колеса мають абсолютно однакові робочі діаметри, чого, звичайно, не буває. В дійсності діаметри oпopно-ходових коліс різні в нормативних межах, колії встановлені з відхиленнями, металоконструкції мають розміри в межах допусків.
В практиці проєктування i експлуатації металоконструкцій вантажопідйомних кранів існують випадки, коли конструкція протягом одного робочого циклу може змінювати характер своєї статичної визначеності.
В процесі експлуатації чотирьохопорна пласко-просторова рама мостового крана має в умовах експлуатації в кожному конкретному положенні вантажного візка вздовж прогону крана фактично три конкретні точки опори, тобто має статичну визначеність, комбінація i вид якої у залежності від переміщення візка з вантажем може змінюватися. При pyci візка назад попередня комбінація опорних точок відновлюється. Сполучення опорних точок також постійно змінюється i відновлюються під час руху мостового крана з вантажем вздовж підкранової колії. Отже, під час переходу візка з вантажем через критичне положення відбувається миттєве обертання моста крана відносно його діагональної вісі. Тобто, відбувається зміна статичної визначеності кранових балок. При обертанні моста вибирається зазор між колесом, яке до цього не було опорним, та підкрановою рейкою i в ту ж мить утворюється зазор під діагонально-протилежним колесом. Вказані зазори є результатом допускної та експлуатаційної нерівномірності діаметрів ycix чотирьох опорно-ходових коліс, експлуатаційного зносу коліс, нормативного i не нормованого відхилення підкранової колії від горизонтальності з експлуатаційних причин, а також допускних відхилень розмірів металоконструкції моста при його виготовленні. Ці зазори особливо відчутні для короткопрогінних i жорстких мостів i менш суттєві для довгих та податливих мостів.
На рис. 1 приведено два положення чотириопорного вантажного візка вздовж мосту. Припустимо, що в першій позиції пласко-просторова рама мосту опирається на опорно-ходові колеса A1, A2,В2. Між колесом B1 i рейкою є зазор δ, який утворюється за рахунок нормативних відхилень рівнів по вертикалі кожної підкранової рейки, а також експлуатаційної різниці діаметрів опорно-ходових коліс крана.
Після переходу точки O1(центра ваги візка) через точку О (центр діагоналей мосту), тобто візок переходить в другу позицію, відбувається миттєве обертання моста крана навколо діагоналі A1,B2, i балка 1 перетворюється з консольної на двоопорну, а пласко-просторова рама мосту отримує опорний контур A1,B1,B2, змінює конфігурацію своєї статичної визначеності.
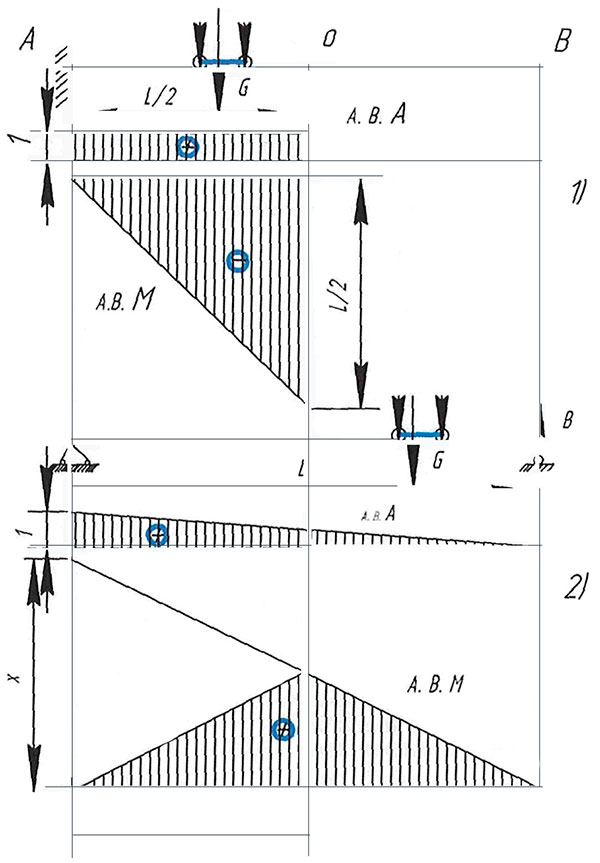
Для першого положення головна балка 1, як основний несучий елемент, є консольною. При подоланні вантажним візком критичного положення головна балка миттєво стає двоопорною статично-визначеною. Відповідно, лінії впливу реакцій oпop А, згинальних моментів Мmax для балки змінюють свій характер (рис. 2). В цю ж мить лінія впливу згинального моменту Мmax головної балки, як основного розрахункового фактора, змінює знак на протилежний. Якщо для консольної балки верхній пояс є розтягнутим, а нижній — стиснутим, то для двоопорної балки, навпаки, верхній є стиснутим, а нижній — розтягнутим. За повний цикл переміщення візка вздовж такої балки її верхній i нижній пояси завантажуються знакозмінними циклами з напруженнями, близькими до симетричних циклів. Часто при експлуатації малопрогінних кранів великої вантажопідйомності з важкими режимами роботи спостерігається наявність поперечних втомних тріщин як на верхніх, так i на нижніх поясах, що є доказом присутності в поясах знакозмінних напружень. Ці обставини слід враховувати при розрахунках головних балок на втому.
Статистичні данні по пошкодженнях i тріщинах металоконструкцій свідчать про те, що місце пристиковки головної балки до кінцевої є найбільш вразливе i таким, де виникає більшість втомних тріщин. Для двоопорної балки характер розрахунків на втому добре відпрацьований i відомий.
3 метою уникнення статичної невизначеності кранових мостів зараз пропонуються різні конструктивні заходи, які є малоефективні та невиправдані із затратних міркувань. Крім того прагнення уникнути статичної невизначеності пласко-просторової рами моста вантажопідйомного крана однозначно призводить до статичної невизначеності пласко-просторової рами вантажного візка. Відбувається декомпозиція зазорів пропорційно співвідношенню геометричних розмірів моста крана i візка.
Рекомендується для короткопрогінних (до 20м) мостів вантажопідйомних кранів, які працюють у режимах A5...A8, виконувати розрахунок місць пристиковки головних балок до кінцевих oпop на втому від знакозмінних напружень, які виникають в результаті зміни характеру статичної визначеності пласко-просторових рам кранових мостів за кожний повний цикл роботи крана.
Необхідно також дотримуватись при експлуатації вантажопідйомних кранів нормативних відхилень стану підкранових та підвізкових рейок, не перевищувати допускних відхилень при виготовленні та монтажу ходових коліс та металоконструкцій вантажних візків.
Під лінією впливу прогинів (переміщень) розуміється геометрична залежність прогинів будь-якого зафіксованого поперечного перетину балки від положення на ній умовного одиничного рухомого навантаження. Тобто, лінія впливу прогинів балки показує як змінюється пружна крива лінія прогинів балки від зміни положення умовного рухомого одиничного навантаження вздовж балки.
Для визначення прогину в будь-якому перетину балки, особливо важливо знати максимальний прогин балки, що є величиною підконтрольною, яка нормується статичною та динамічною жорсткістю балки, рекомендується побудувати лінію впливу прогину балки, для чого зручно скористатися методом Mopa, або інтегралом Mopa, що більш відомий термін в інженерній теорії та практиці.
Прогин балки залежить від моменту згину, як внутрішнього силового фактора, що виникає від зовнішнього навантаження. В загальному вигляді інтеграл Mopa є
- де Мр — епюра згинаючого моменту в фіксованому перетині балки від зовнішнього навантаження, кНм;
- М1, — епюра згинаючого моменту від дії зовнішнього одиничного навантаження (одинична епюра), прикладеного до місця та напряму визначаємого прогину, 1·м;
- Е = 2,1х105 — модуль пружності першого роду, MПa;
- Jx — момент інерції поперечного перетину балки в місці прогину, м4.
Для практичного визначення прогину статично визначених балок зручніше користуватися методом Верещагіна
- де ω — площа криволінійної епюри згинаючих моментів від зовнішніх сил, кНм2;
- ус — ордината епюри згинаючого моменту від одиничної сили, що лежить проти центра ваги криволінійної епюри, м.
Для кранової балки, завантаженої комплексом стаціонарних та рухомих навантажень краще побудувати лінію впливу прогинів для розрахункових перетинів балки.
В інженерній практиці часто виникає необхідність визначення прогинів в різних точках балки, наприклад, при дослідженні статично невизначених балок велике значення мають прогини її в різних точках прогону aбo вильоту, aбo у випадках, коли максимальний прогин балки має бути обмеженим нормативною (допускною) величиною.
При статичному навантаженні пружна лінія прогину балки має криволінійну форму. Розглянемо як змінюється крива прогину балки, завантаженої рухомим навантаженням, для цього спробуємо побудувати лінію впливу прогину балки. В сучасній інженерній практиці проєктування та дослідження кранових балочних конструкцій не відомі приклади побудови ліній впливу прогинів балки.
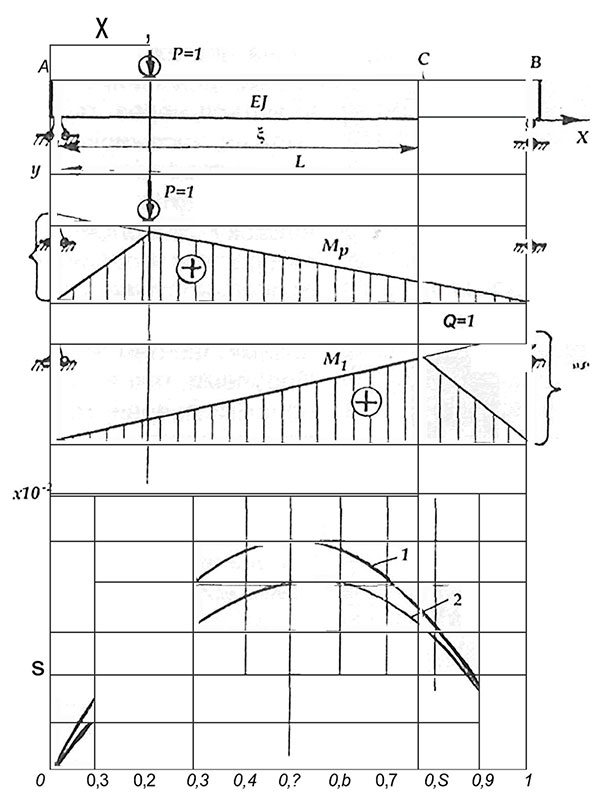
На розрахунковій схемі (рис.3) розглядається перетин "С" двоопорної балки, в якому необхідно визначити прогин Y. Згідно інтеграла Mopa для визначення прогину в точці "С" під дією зовнішнього навантаження Р рекомендується прикласти в цьому перетині одиничне навантаження Q=1 в напряму дії прогину.
В якості зовнішнього навантаження до балки прикладаємо одиничне рухоме навантаження P=1. Тоді, побудувавши епюри Мp та M1 можна визначити прогин балки в перетині "С" . Максимальні поточні значення моментів дорівнюють
Тоді прогин балки в перетині "С" дорівнює
При цьому слід враховувати дві дільниці балки, перша — до перетину "С" , друга — після перетину "С" для одиничної епюри M1. Також різними будуть функції моментів від зовнішнього навантаження P=1 для першої ділянки балки — від 0 до поточного положення х, та другої — від х до L.
На рис. 3 приведені лінії впливу прогину балки у відносних одиницях для перетину балки С. Крива 1 відповідає лінії впливу для перетину балки, що розміщений в середині прогону. Крива 2 — перетин балки знаходиться на відстані ξL= 0,7 від опори А.
Зважаючи на одиничне рухоме зовнішнє навантаження P=1, положення якого є змінною вздовж балки величиною, можна визначити лінію впливу прогину для кожного перетину. Якщо ж розглядати розміщення перетинів на балці як поточно змінну величину, то отримаємо спектр ліній впливу прогинів балки конкретної жорстокості.
Як видно з дослідження, лінії впливу внутрішніх силових факторів, прогинів, систем із змінними параметрами є потужним засобом дослідження кранових балок, завантажених комплексом рухомих i стаціонарних експлуатаційних навантажень. 3 метою удосконалення методів прецензійного більш точного проєктування кранових металоконструкцій необхідно продовжити дослідження в напряму роботи телескопічних, статично невизначених кранових балок, стріл та фермених конструкцій за допомогою ліній впливу, в екстремальних умовах експлуатації.
Заключення
Дослідження показали, що використання ліній впливу для аналізу роботи кранових балок під час переміщення навантажень є ефективним методом для підвищення точності розрахунків. Такий підхід дозволяє детально оцінювати напруження i деформації в конструкціях, що важливо для забезпечення ïx надійності та безпеки. Подальший розвиток цього напрямку сприятиме вдосконаленню проектування та експлуатації вантажопідйомних механізмів, що в свою чергу підвищить ефективність i безпеку в галузі.
